This problem examines viscous fluid flow in a 2D channel. FlexPDE solves for the X- and Y- velocities of a fluid, with fixed pressures applied at the ends of the channel. The reynolds number in this problem is approximately 20.
The Navier-Stokes equation for steady incompressible flow in two cartesian dimensions is
rho*(dt(U) + U*dx(U) + V*dy(U)) = mu*div(grad(U)) - dx(P)
rho*(dt(V) + U*dx(V) + V*dy(V)) = mu*div(grad(V)) - dy(P)
together with the continuity equation,
dx(U) + dy(V) = 0.
Here U and V are the X- and Y- velocities, P is the pressure (introduced as a surrogate for the continuity equation), rho is density, and mu is viscosity.
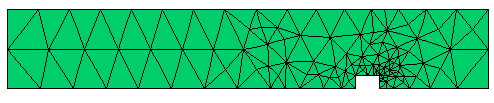
Adaptively refined mesh:
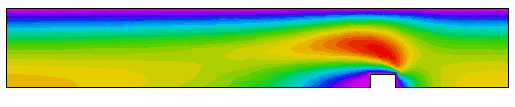
Fluid Speed:
Pressure:

