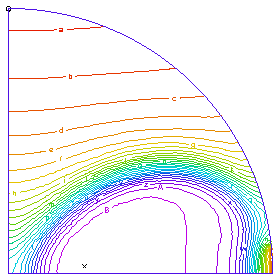
Example : Chemical ReactionsThis problem follows a cross section of the gas in an open tube chemical reactor as the gas flows down the tube. The chemical reaction has a reaction rate which is exponential in tempreature, and shows an explosive reaction completion once the 'ignition' temperature is reached. There is a heated band on each side of the tube, to help induce ignition. We model one quarter of the circular cross section. There are two simultaneous PDE's, one for the temperature and one for the chemical concentration:
dt(T) = div(grad(T)) + a*(1-C)*exp(G-G/T)
dt(C) = div(grad(C)) + b*(1-C)*exp(G-G/T)
Here T is the temperature, C is the concentration. a, b, and G are constants.
|
|
|
A profile of the temperature distribution as the burn front propagates across the tube. (Time = 0.25 sec) |
|
|
|
|
|
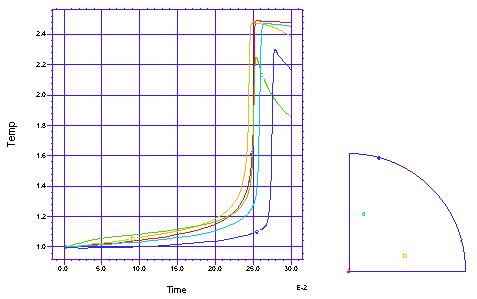
The history of temperature at several points in the tube |
